研究の概要
可逆コンピューティング
物理学の基本原理である可逆性や(エネルギーなどの)保存性を反映した計算モデルを研究しています.AND, OR, NOT のような従来型素子とは全く異なる演算方式の可逆論理素子を発案し,また,種々のタイプの可逆コンピュータの構成法を示しました.
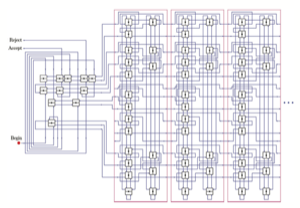
(可逆論理素子によって構成された計算機モデル)
セルオートマトン
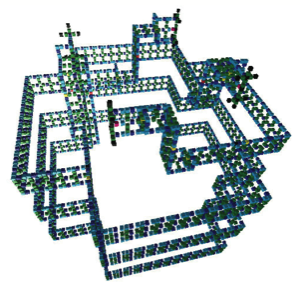
(3次元セルオートマトンによる形態形成)
セルオートマトンとは,ごく単純なコンピュータを非常に多数,規則正しく配置・接続したような計算システムのモデルです。将来,ナノテクノロジーの発達によって,信号の伝達や操作の機能を持つ分子を多数,自在に結合させた物質を作り出せるようになるでしょう.セルオートマトンを用い,どのような機能性分子をどのように結合すれば全体として高性能のコンピュータとして働くかを研究するための基礎となる理論の構築をめざしています.
計算の複雑さの理論
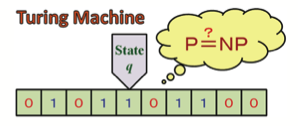
(2)どのような問題が,チューリングマシンで多項式時間で解けるP問題なのか,また,どのような問題が,効率的な時間では解けないとみられるNP完全問題なのかを調べています.コンピュータサイエンスの有名な未解決問題「P=NP質問」の解決への糸口を探究しています.